
DNA濃度、RNAの濃度、タンパク質の濃度を測定する時に欠かせないのが「吸光度法」。
「吸光度法」を語る上で知っていなければならないのが、「ランベルト・ベールの法則」です。
この記事では、「ランベルト・ベールの法則の導出方法」を簡単にまとめていきます。
ランベルト・ベールの法則とは?
そもそも、ランベルト・ベールの法則とはなんなのでしょうか?
ランベルトの法則とベールの法則を足し合わせたものです。
ランベルトの法則もベールの法則も溶質に光を当てた時に、溶質がどれくらい光を吸収するのかを調べたもの。
ランベルトの法則(1760年ごろ)は、溶質の長さと光の吸収が比例するという法則。

ベールの法則(1850年ごろ)は、溶質の濃度と光の吸収が比例するという法則。
溶質の長さ(l)を一定としたときの単色光(一つの波長の光)に対する吸光度(入射光と透過光の比の対数)(A)はその物質の濃度(c mol/L)に比例する。
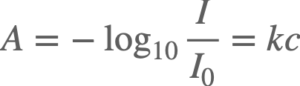
ランベルト・ベールの法則は、溶質の吸光度(入射光と透過光の比)は溶質の長さと濃度の積に比例するという法則。
一般的にはこのような式で表されます。
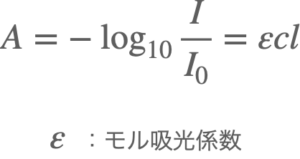
この時の比例定数(ε)はl = 1 cmの時の希薄溶液に対する単位濃度あたりの吸光度を示しています。
この法則が成り立つ条件としては、
- 入射光は一波長であること(単色光)
- 溶質の表面で反射がないこと
- 溶質中で光が散乱しないこと
- 溶媒が均一であること
- 希薄溶液であること
などが挙げられます。
この条件に当てはまらない場合は、標準溶液を使って検量線を描いて測定する必要があるので注意が必要です。
生命科学では、物質(核酸やタンパク質)の濃度はこの法則を当てはめて測定しています。
教科書ではランベルト・ベールの法則の式しか示されないことが多く、どのように導出するかは書いてありません。
ランベルト・ベールの法則がどのように導出されるか見ていきましょう。
ランベルト・ベールの法則の導出方法
ランベルト・ベールの法則は、ランベルトの法則とベールの法則を二つ組み合わせたものだということがわかりました。
それぞれの法則の式はどのように導出されるのか、見ていきましょう。
ランベルトの法則を導出する
ランベルトの法則は、溶質の長さと光の吸収が比例するという法則でした。
ある溶質Xの長さがxの時に光が20%吸収される場合、どうなるかを考えてみます。
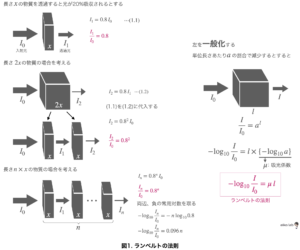
左の例を、一般化するとランベルトの法則の式が導出されるというわけです。
ランベルトの法則を一般化する時に、両辺に負の常用対数を取っていました。
なぜ、負の対数を取るのか?下の図を使って考えてみます。
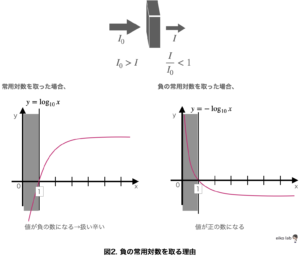
正の対数を取ると入射光と透過光の比が必ず1よりも小さくなり、値が負の数になってしまいます。
負の数は扱い辛いので、値を正の数にするために負の対数を取るのです。
もしくは、入射光と透過光の分子と分母を入れ替えるというのも一つの手です。
ベールの法則を導出する
ベールの法則は、溶質の濃度と光の吸収が比例するという法則でした。
溶質の断面積を100、溶媒分子の断面積を1としてどのように光が吸収されるのか考えてみましょう。

ベールの法則の式が導けました。
ランベルト・ベールの法則を導出する
では、最後に上記の二つを合わせたランベルト・ベールの法則を導出しましょう。
導出方法はこちらのサイトを参考にしました。(ベールの法則をベースに考えていきます)
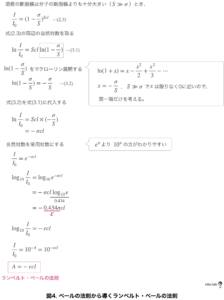
図3の式2.3から出発して式を導出していきます。
式2.3の両辺の自然対数を取って展開していきます。
(常用対数を取らないのはマクローリン展開をするために常用対数ではなく自然対数にします)
〜生命科学系のための補足〜
最初に使ったマクローリン展開とは?少しだけ補足しておきましょう。
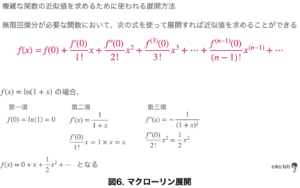
以上、ランベルト・ベールの法則の導出でした。
他の導出方法としては、微小区間での変化を考えて微分方程式を立てて解いていく方法もあります。















