
二つの変数に関連・関係性があるかどうかを言うためには、「相関係数を計算する」と言うステップを踏みます。
科学の論文などでは「濃度依存的に遺伝子の発現が変化する」と言いたい時には、ただ棒グラフや散布図を見せるだけではなく、「薬剤の濃度」と「遺伝子の発現量」の相関係数を計算する必要があります。
他にも「ある2つのタンパク質の共局在」を示したい時にも、2つのタンパク質を別々の蛍光で染めて写真を撮って蛍光シグナルの位置が一致していることを言う時にも、相関係数を計算することで数値データとなって説得力が増します。(画像解析・共局在解析に関してはまた別の記事にまとめようと思っています)
相関係数と言えば、「ピアソンの積率相関係数(Pearson correlation coefficient)」が一般的によく使われています。その他にも「スピアマンの順位相関係数(Spearman's rank correlation coefficient)」や「ケンドールの順位相関係数(Kendall rank correlation coefficient )」があるのをご存知ですか?
この記事ではピアソンの相関係数とスピアマンの相関係数を中心に、「相関係数」について簡単にまとめて行こうと思います。
「相関がある」とはどういうことなのか?
そもそも、「相関がある」とはどう言うことなのでしょう?
「相関」を辞書(新明解第七版)で引いてみると...
二つのものが密接に関係を持っていること。
「ー関係」一方が変化すると、他方もそれにつれて変化するという関係
とあります。
しかし、英語の「correlation」は二つのものが「線形」の相関を持っていることを表す言葉のようです。
「線形の相関」とは、xy平面上に二つのものの関係をプロットしたときに、"y=ax+b"の一次式で表されると言うこと。直線的な関係があることを「線形の相関がある」と言います。
ピアソンの積率相関係数も、スピアマンの順位相関係数もこの二つのものの線形的な関係の強弱を表したものなのです。
ピアソンの積率相関係数とスピアマンの順位相関係数の違い
「相関係数」といえば「ピアソンの積率相関係数」と「スピアマンの順位相関係数」が一般的に用いられますが、何がどう違うのでしょう?
違いを簡単にまとめると...
-
- パラメトリックな相関係数でデータが正規分布するときに用いられる
- 値の絶対値が1に近いほど相関が強いことを表す
-
- ノンパラメトリックな相関係数で正規分布しないデータで用いられる
- 2つの変数の2つのパラメータの値の順位で評価する
- 「一緒に変化するか」は評価できるが、それが一定の割合かどうか(線形の関係かどうか)はわからない
文字で見ていてもイメージが湧きにくいと思うので、図にまとめてみました。

左のグラフのように直線的な比例関係であれば、ピアソンの相関係数もスピアマンの相関係数も1になり(グラフが右下がりであれば-1になります)、全く相関がなければ0に近づきます。
しかし、真ん中の図のように変数1と変数2で増加の関係があるとしても、直線関係でなければピアソンの相関係数は1より小さくなります。それに対し、スピアマンの順位相関係数は変数1が増えれば変数2も増えるており、「一緒に変化」しているので1になります。
相関係数は求めるだけで終わりではありません。「相関係数が0.9だから強い相関があります」とはまだ言えません。求めた相関係数から「本当に相関があるかどうか」を検定する必要があるのです。
と言うことで、相関係数を求める手順としては
-
- 散布図でデータを可視化する
- 帰無仮説・対立仮説を立てる
- 相関係数を計算する
- 検定表で相関があるかどうかを検定する
そのことを踏まえた上で、ピアソンの積率相関係数とスピアマンの順位相関係数の求め方を見ていきましょう。
ピアソンの積率相関係数の求め方
ピアソンの積率相関係数は具体的にどのように求めるのでしょう?相関関係を求める手順にしたがって求め方を紹介していきたいと思います。
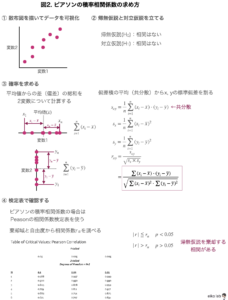
-
- 散布図でデータを可視化する
x軸に変数1、y軸に変数2を取り、散布図を描くとデータのばらつき具合がわかりやすい - 帰無仮説・対立仮説を立てる
「相関がない」(可能性が高いこと)を前提に検定を行うので、帰無仮説を「相関がある」、対立仮説を「相関がない」とします。 - 相関係数を計算する
ピアソンの積率相関係数の場合は、「データの平均値からどれくらい離れているか?」を基準に(生データの数値を使って)統計量を算出していきます。(エクセルやR、PSPP、SASなどで計算できます) - 検定表で相関があるかどうかを検定する
算出できた統計量と検定表の数値を比べる。計算してきた統計量の方が大きければ帰無仮説は棄却されて「相関がある」となります。
検定表は自由度と棄却領域によって数値が並んでいます。
- 散布図でデータを可視化する
スピアマンの順位相関係数の求め方
では、ノンパラメトリックであるスピアマンの順位相関係数はどのように求めるのでしょう?
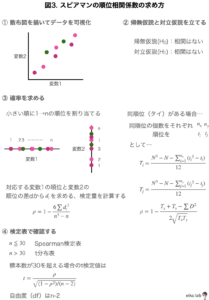
ピアソンの積率相関係数は生の数値データを使うのに対し、ピアソンの順位相関係数は順位に変換して検定量を計算します。(生のデータを順位に置き換えるのはノンパラメトリックな検定でよく行われますね)
基本的な手順はピアソンの相関係数と同じですが、最後の「検定表で確認する」が少し異なります。標本数が小さいときにはSpearmanの検定表を使いますが、多くなってくると(標本数20〜30)統計量が近似的にt分布に従うためt分布表を使うようです。
ピアソンの積率相関係数とスピアマンの順位相関係数 まとめ
最後にピアソンの積率相関係数とスピアマンの順位相関係数について簡単にまとめておきましょう。
- ピアソンの積率相関係数はパラメトリック、スピアマンの順位相関係数はノンパラメトリック
- ピアソンの積率相関係数は「線形な関係があるか」どうかを検定する
- スピアマンの順位相関係数は「一緒に変化するか」どうかを検定する
ちなみに、ケンドールの順位相関係数はスピアマンの順位相関係数と同様にノンパラメトリックな手法で傾向も似ているようです。














