
私たちに身近なグラフといえば、日々更新される新型コロナウィルスでの新規感染者の推移となってしまいましたね。
このグラフは推移を表していて数値は一つに決まってしまうのでエラーバーはついていません。
しかし、科学の世界ではエラーバーがついていないデータは信用に値しないとみなされてしまいます。
エラーバーに標準偏差(SD)と標準誤差(SE)の二種類あって、どちらの値でエラーバーをつけたら良いか悩んでしまう人が結構います。
生命科学系の雑誌では標準誤差が使われることが多いのですが、「なんで標準誤差にしたのか?」きちんと説明できない人も中にはいます。(「研究室のみんなが標準誤差を使っているから」とか「なんとなく」とか「標準偏差よりもエラーバーの幅が小さくてカッコ良いから」とか...)
「標準偏差と標準誤差の違い」を知っておくと、自分がデータを示すとき、他の人のデータを読むときに役立つことは間違い無しです。
標準偏差と標準誤差をどのように使い分けたら良いか?を中心にまとめていきましょう。
標準偏差と標準誤差はどう使い分ければ良いの?
結論から言えば、「データを示すときに何を言いたいのか?」によります。
データのバラつきを具合の大きさを言いたいのか?
実験の再現性の高さを言いたいのか?
2群の平均値の違いを示したいのか?...
それによってデータに標準偏差と標準誤差どちらを使うかが変わってくるのです。
と言うことは、標準偏差とはどう言うものか?標準誤差とはどう言うものか?の両方をを知っておく必要がありますね。
標準偏差とは?
標準偏差は英語で言うと、Standard Deviation(SD)。
standardは「基準」、deviationは「逸脱」などと訳されますね。要はある基準からどの程度(データが)外れるか(離れているか)、得られたデータのバラつき度合いをを表すのが標準偏差です。
標準偏差はデータの分散の平方根で表されます。
標準偏差の計算のしかた
標準偏差はデータの分散の平方根で表されるということでした。具体的にどういうことなのでしょう?
ある遺伝子改変したマウスの5週齢の雄の体重を12匹分測定したとします。データは12個で平均値が1つ算出されます。

サンプル数が十分大きい場合(いくつ以上というのは正確にはありません)、データの分布が正規分布に近似するので
(データの平均値)±2SD
にデータが95%の確率で入ります。
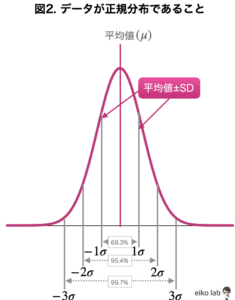
つまり、標準偏差はデータのバラつきが正規分布であることを前提に表される指標なのです。標準偏差と正規分布は密接な関係があることを頭に入れておきましょう。
サンプルサイズが小さくて、データの分布が正規分布では無い場合どうしたら良いのでしょうか?
生命科学の実験の場合、同じ実験を3〜4回繰り返して一つのデータとすることが多いのが現実。
同じ実験を10回も20回もできません。
...ということは必然的にサンプルサイズが小さくてデータの分布が正規分布では無い場合が多くなります。
それでも平気でエラーバーに標準偏差を使っている人がいて、科学雑誌側がきちんと統計を勉強してデータを示すように指導するようになってきたのが最近の現実です。
さて、サンプルサイズが小さくてデータの分布が正規分布では無い場合はどうしたら良いのでしょう?
データのばらつき度合いを示す指標として、中央値とパーセンタイル値を使います。
詳しい説明は割愛しますが、要は「箱ひげ図」を使ってねということ。
(「箱ひげ図について」は別記事で紹介する予定です)
エラーバーに標準偏差を使うとき
もう一度振り返ると、標準偏差とは「得られたデータのバラつき度合い」を表す指標でした。
具体的にどんなときに標準偏差を使えば良いのでしょうか?
・医学系論文でサンプリングした人たちのバックグラウンドのばらつきについて示したいとき
・一回の実験で複数のサンプルを採取して一つのデータにしたいとき(生命科学系の実験ではNGですが...)
などでしょう。
標準誤差とは?
標準誤差は英語で言うと、Standard Error(SE)。
standardは「基準」、errorは「誤り」と訳されます。要はある基準の範囲を示して、その中に真の値(母集団の平均値)が入る確率が高いことを表したのが標準誤差です。
標準誤差は標準偏差をサンプル数の平方根で割ったもので、必然的に標準偏差よりも小さくなります。
エラーバーの範囲が小さくなり、カッコ良いグラフが描けるので好んで使う人が多いのですが、何を表したいのかきちんと理解した上で使うようにしましょう。
そもそも、
- 母集団ってなんでしょう?
- なぜ標準偏差をサンプル数の平方根を割ったものが母集団の平均が入る確率が高い区間になるのでしょう?
- 母集団の平均が入る確率が高い区間を示したいときってどんなときでしょう?
その疑問を解決しながら、「標準誤差」についてまとめていきます。
母集団って何?
母集団とはこれから調べたいと思っている集団の全体のこと。
例えば、「東京都民の身長の平均を調べたい」と思ったときには「東京都民全員」が母集団となります。
しかし、母集団全てについてデータを取るのはなかなか難しいのが現実。
東京都民の人数は140万人ほどと有限な数ですが、全ての東京都民の身長を測定して回るのは結構大変ですよね。
そこで統計の世界では、母集団の一部を選んでデータをとって母集団について推測する(統計的推測)を行うのです。この母集団の一部のことを標本と言います。
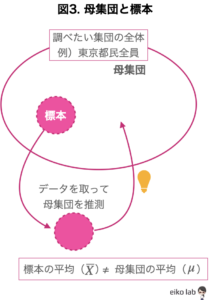
実験の世界では、「標本を抽出して母集団を推定する」が基本になってきます。
そこで注意しておきたいのは、標本は母集団の一部をとってきて調べるので母集団を調べるときには起こらない「誤差」(抽出誤差)が生じてきます。
その誤差の範囲を表したのが「標準誤差」なのです。では、どのように計算すると母集団との誤差を調べることができるのでしょう?
なんで標準誤差は標準偏差をサンプル数の平方根を割ったものになるのか?
確認しておきたい大前提として、無作為に抽出してきた標本の平均の値と母集団の平均の値にはズレがあります。
そこで、母集団の平均がどれくらいの幅の中にどれくらいの確率で存在しているのか推定していくことで、母集団について知ることができるのです。
では実際にどのように計算すれば求められるのかまとめていきましょう。
ある遺伝子改変したマウスの5週齢雄マウスにおける体重の平均を調べたいとします。
遺伝子改変したマウス全数を調べるのは不可能なので、何匹かのマウスを選び出して体重を測定し、母集団の平均値を推定していきましょう。
一回に生まれてくる雄マウスの数は限られているので、3匹ずつ10回、合計で30匹分のデータを取ったとします。(30個のデータと10個の平均値が得られました)
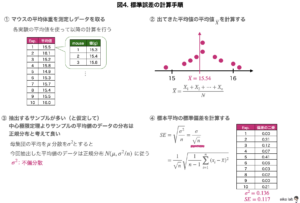
図4を見ていただければお分かりかと思いますが、「中心極限定理」を使うと母集団から標本を抽出する回数が多いとそれは正規分布だとみなすことができます。
標本平均の標準偏差を求めることで、母集団の平均が入る確率の高い範囲を推測できるということ。
平たい言葉で言うと、標準誤差は標本平均の標準偏差だと言うことができます。
エラーバーに標準誤差を使うとき
では、エラーバーに標準誤差を使うのはどのような時でしょう?
標準誤差は、「母集団の平均値が入る推定範囲」を表す指標でした。
母集団の平均値を示したいときに標準誤差を用いるのが適切です。
例えば、
・薬剤投与したものとしていないもので平均値に差があるかどうかを比較したい
・遺伝子を強制発現させた場合とそうでない場合、ノックダウンした場合を比較したい
などでしょう。
実験する上で注意したい標準偏差と標準誤差
散々、難しい話をして「標準偏差と標準誤差の違い」を説明してきました。
私自身、色々な統計の教科書やネットの解説ページなどを見て回ったのですが、結局文字で書かれていてもよくわからないでモヤモヤしたままで理解したつもりになっていた部分もあります。
生命科学系分野で実験してデータを出す人のために、「標準偏差と標準誤差の違い」をおさらいしておきましょう。
生命科学系分野で基本的に示したいことは、「複数の群を比較して平均値に”差”があるかどうか」です。
なので棒グラフを書いてエラーバーをつけるときには「標準誤差(SEM)」を使うのがスタンダードだと思っておきましょう。
そこで振り返っておきたいのが、「標準誤差」を計算するときに使った「中心極限定理」です。
「中心極限定理」は、母集団から抽出した標本の数が多ければその平均値の分布は正規分布に近づくと言うもの。
つまり実験試行回数がある程度必要だと言うことなのです。(具体的にはよくわかりませんが、最低3〜5回は必要なのではないかと言う感覚を持っておくと良いでしょう。)
「標準誤差」は各実験の平均値を使って算出するものでした。
なので、1回の実験で10個のサンプルからデータを抽出して一つのデータを作るときに「標準誤差」を使うのはあり得ないと言うこと。(1回の実験しかしていないのですから...)
同じ10個程度のサンプルを扱うにしても、3個のサンプルからデータを抽出する実験を3回行うことで「標準誤差」を使ってより正確に「母集団の平均」を割り出すことができるのです。(実験の再現性も確認できるので一石二鳥ですよ)
正規分布であることに注意!
「標準偏差」の概念はデータの分布が正規分布であることを前提に成り立っています。
(「標準誤差」も平均値の標準偏差なので正規分布であることが前提です)
「データの数、サンプルの数が多ければ」、正規分布であると言って良いとして教科書では話が進んでしまいます。
しかし、「多ければ」ってどれくらい多ければ良いのでしょう?
5は多い?10はないとだめ?いやいや30でしょう!とかなり曖昧な定義だと言うことがお分かりになると思います。
棒グラフに標準偏差や標準誤差などのエラーバーをつけてデータを示したいのであれば、データの正規性を確認するようにしましょう。
そうでない場合は一つ一つのデータの値を示すか、データの分布がわかるように最大値、最小値、中央値、パーセンタイル値を使った箱ひげ図が推奨されています。
今後は棒グラフ+エラーバーと言うグラフではなく、箱ひげ図が増えてくるかもしれませんね。
標準偏差と標準誤差の違いまとめ
最後に、標準偏差と標準誤差の違いをまとめておきます。
- 「標準偏差」は生データを使って計算し、データのバラつきを示すもの
- 「標準誤差」はデータの平均値を使って計算し、母集団の平均値が入る確率の高い範囲を示す
- 「標準偏差」も「標準誤差」もある程度データの数が多くなければならない
- 最近は箱ひげ図を使ってデータの分布を示すことが多くなってきている















