
実験を始めるときに、実験検体の数(サンプルサイズ)ってどうやって決めていますか?
なんとなーく「Nは3より大きい方が良い」という雰囲気はあるような気がしますが、「in vitroは3くらいで良くてin vivoは7以上あった方が良い」と言う基準の人もいます。
このサイト内で仮で行っている「薬剤Aと言う薬が細胞Xの増殖を促進するかどうか?」を検証する実験のサンプルサイズの決定は妥当なのでしょうか?
検証して行きましょう。
実験を始める前にしておくこと
『実験計画の立て方』でも書いてありますが、実験前に決めなければいけないことは沢山ありますよね。
どんな統計処理をするか?サンプルサイズはどれくらいにするか?も全て実験前の計画段階で決めておく必要があるものなのです。
おさらいになりますが、『実験』は「何かの仮説を証明する」ために行います。
「何かの仮説」とは、「Aという薬が細胞Xの増殖を促進するのか?」とか「AとBではどちらが薬剤効果が高いのか?」、「遺伝子Gは組織Yの形成に影響を与えるのか?」などなど...要は「何かと何かに違いがあるかどうか?」を示すことが必要になります。
「何かの仮説」を証明するために『実験』をして、データを取ります。
取ってきたデータを元に統計学的に検定(統計的仮説検定)をすることで、「違いがあるのかどうか?」を示して行きます。
検定をするときに、「違いがあるかどうか?」の基準をあらかじめ決めておかなければなりません。
この基準を決めるときにサンプルサイズも決めることになります。
今回は直感的に下記のように決めました。

実験前にやることをまとめるとこのような感じになります。

実際にデータを取った結果がこちら。
計数した結果、15枚中15枚で数が増えていました。

あらかじめ決めた基準では、「増殖した」と言うことになります。
この基準を満たすのは「偶然起こった」ことかもしれません。
どれくらいの頻度で偶然起こることなのかを見積もって行きます。
これを「統計学的処理」と言います。

直感的に決めた「基準」が妥当なものなのか?検証してみましょう。
決めた「基準」がどれくらいの確率で起こるのか?
今回の場合、
「薬剤Aを添加した場合、細胞数が増える」
ことを示したいと思っています。
帰無仮説(null hypothesis)は、
「薬剤Aを添加しても細胞数に影響を与えない」
となります。
帰無仮説が正しいとした場合の確率分布を描いてみると...
(このグラフの描き方は別の記事にまとめる予定です)
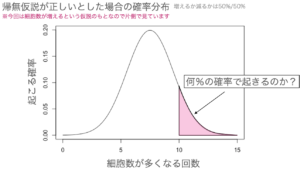
増えるか、減るかの確率が半々の場合の確率分布の具体的な数値は以下のようになり、10枚以上で増える確率は、

15%以上になることがわかりました。
この帰無仮説が正しいとした場合に、示したいと思っていることがたまたま起こる確率をp値、有意水準と言います。
(有意水準に関しては詳しく別の記事にまとめます)
実験の世界では慣習的に有意水準は5%以下とされる場合が多いので、今回設定した基準が15%とかなり高いことがわかりました。
有意水準を5%以下とした場合、
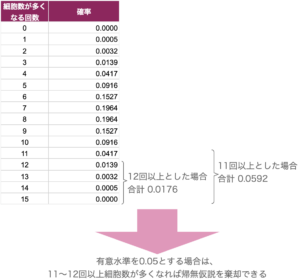
12枚以上で増えれば、帰無仮説を棄却でき、「増加した」と言ってもよさそうです。
基準を書き換えてみましょう。

15枚のデータを取ってきて、12枚で増えていれば有意に増加したと言えそうですね。
ところで、サンプルサイズ適当に決めた15枚で良いのでしょうか?
サンプルサイズの妥当性を考える
15枚写真の写真について、解析を行うことにして、そのうち12枚で増加していれば「薬剤Aは細胞Xに対して増殖促進作用がある」と言ってもよさそうです。
15枚と言う数は直感的に決めたものですが、妥当なのでしょうか。
このときに出てくる考え方として、「検出力」と言うものがあります。
検出力は、簡単に言うと「増加しているものをちゃんと「増加している」と言える確率」のことです。
もう少し詳しくみてみましょう。
90%の確率で増加する場合の確率分布を考えます。
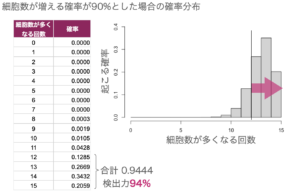
12枚以上とした場合、94%の確率で「増加した」と言えます。
しかし、80%の確率で増加する場合ではどうでしょう?
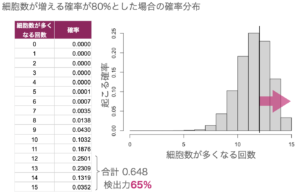
12枚以上とした場合、65%の確率でしか「増加した」言えなくなってしまいます。
つまり、正しい判断ができる確率が下がってしまうのです。
この場合どうしたら良いでしょうか?
この「検出力」はサンプルサイズに依存します。
解析する枚数を倍の30枚にしてみましょう。
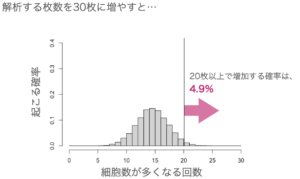
有意水準を5%に設定すると、20枚以上で増加が見られれば「増加した」と言ってもよさそうです。
ここで、80%の確率で増加する場合を見てみましょう。
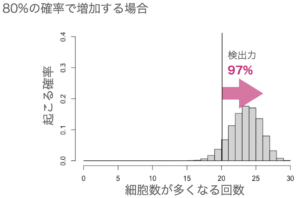
検出力が97%にまで上がりました。
サンプルサイズが15だと90%の確率で増加する場合は94%で見破れます。
サンプルサイズが30だと80%の確率で増加する場合は、97%で見破れるようになります。
と、ここまでは教科書的な話です。
サンプルサイズと実際の実験系について考える
サンプルサイズを稼ぐために、1個のサンプルから15枚も30枚も写真を撮るのでは意味がありません。
通常は、1個のサンプルから3〜5枚写真を撮ってその平均値を1つのデータとします。
このことからわかるように、生命科学の実験では15回も30回も実験することはほぼありません。
in vitroでもin vivoでもサンプルサイズは5〜10程度というのが普通です。
「最低N=3」と言われるのは、N=3だと最低限の統計学的検定処理ができるようになるからです。
サイズが小さい場合、統計処理を施しても有意な結果が得られない場合もあります。
そのため最近の論文雑誌の流れでは、サンプルサイズが小さいときにはデータを一つ一つプロットして示すのが良いとされています。
一般的に使われるt検定などの仮説検定の考え方は、母集団から取ってきた標本数が十分に多くてデータが正規分布に従う場合という、かなり制約がある検定方法です。
サンプル数が少なくても差を検出する、ノンパラメトリックな検定法使うとよりデータの説得力が増すと考えられます。
どのような統計学的な検定をするかも、実験前に考えておけるとより良いかと思います。
パラメトリックとノンパラメトリック検定についてはこちら
まとめ
この記事のまとめです
- 実験を始める前に、「何を示したいのか?」「判断基準(有意水準)」をあらかじめ決めておく
- 「正しいことを正しいと判断する」(検出力)は、サンプルサイズに依存する
- 生命科学実験の場合、通常は15回も30回も実験することはない
- サンプルサイズが小さい場合は、データ一つ一つをプロットして示す
- サンプルサイズが十分確保できない場合は、ノンパラメトリックな検定法を用いると良い

















