
大学の生命科学系の学科では必ず「(生物)統計学」という講義があって、統計学の基礎は学部生の間に習います。
が、実際に使う場面を想定した講義ではないため、多くの学生さんは試験が終わったらすぐに頭の中から記憶は消え失せてしまうのではないでしょうか?(わたしだけ?)
現役の研究者の中でも、出したデータをなんとなーく統計処理してそれっぽいデータに仕上げてしまっているのでは?と思われることが多い気がします。
この記事では、2群検定の基本である「t検定」を、実験に出て来るようなデータを扱いながら深掘りしていきます。
実験データと検定
2群検定の場合、無意識に“t検定”だからExcelに”=TTEST()”と入れて...とやってしまっていませんか?
細胞Xに薬剤Aを添加したときの細胞増殖能の違いを比べたいと思って、以下の実験をしたとします。
- 細胞Xを同じ細胞数になるように6cmディッシュに播種
コントロール群(薬剤Aの溶媒のみ添加)、薬剤A添加群それぞれ5ディッシュ - 次の日から薬剤Aを添加
- 培養5日目の細胞数計数して比較
1ディッシュあたり5視野を計数
そして、下のようなデータが出ました。

さてどうやって統計処理しましょう?
2群の比較検定だからt検定でOKなのでしょうか?
そもそもt検定ってどんな検定なのでしょう。
実験計画の立て方についてはこちらの記事をご覧ください。
細胞の計数に関してはこちらの記事をご覧ください。
t検定とは?
t検定についてWikipediaを引くと、こう書いてあります。
t検定とは、帰無仮説が正しいと仮定した場合に、統計量がt分布に従うことを利用する統計学的検定法の総称である。母集団が正規分布に従っていると仮定するパラメトリック検定法であり、t分布が直接、もとの平均や標準偏差にはよらないことを利用している。
※帰無仮説:「私たちが立証したい仮説」の逆の仮説
ちょっと教科書的でよくわからないですよね...
例えば、上の実験のようなデータが得られた場合、
「薬剤A添加群とコントロール群で細胞数に差が無い」と言う帰無仮説を立てて、薬剤Aを添加した「母集団の平均値」とコントロールの「母集団の平均値」が等しいかどうかを確率論的に確かめていく。
と言うものです。
母集団や平均についてはこちらの記事をご覧ください。

確率統計学についてはこちらの記事をご覧ください。

t検定を使う上で大切なことは、「母集団が正規分布に従っていると仮定している」と言うこと。(母集団が正規分布に従っていない場合は一般化線形モデルを使用して検討することになるのですが、それはまた別の話)
母集団が正規分布に従っているかどうかは、コルモゴロフ-スミルノフ検定やシャピロ-ウィルク検定などを使って判断することができます。
Rでシャピロ-ウィルク検定をする方法はこちらの記事で紹介しています。

t検定の種類
t検定には大きく分けて3種類に分けられます。
- 1群のt検定
母集団の平均が特定の値であるかどうか?を検定する。
例)50g入りと書かれたポテトチップスに本当に50g入っているのか調べる - 2群のt検定
母集団1の平均値と母集団2の平均値が等しいかどうか?を検定する。
対応のある2群の検定かどうか?分散が等しいかどうか?によって検定方法が異なる。
例)走る前後の血糖値に差はあるのか?を調べる(対応のある2群の検定)
例)薬剤を添加しているかしていないかで差があるのか?を調べる(対応のない2群検定)
対応のない2群の検定には分散が異なることを仮定したt検定(Welchのt検定)を用いるのが一般的になっています。
論文などでよく使われているスチューデントのt検定は、対応のない2群検定で等分散性が仮定できるときのみに使える検定です。
「分散」についてはこちらの記事にまとめています。

片側検定と両側検定
t検定には片側検定と両側検定があります。
一般的には両側検定を選択しますが、なぜでしょう?
両側検定を選択する場合は、母集団の平均値が大きくなるか小さくなるかわからない場合。
片側検定は、実験を始める前からどちらかの母集団の平均値が大きなる(または小さくなる)かわかっているときにのみ行う検定。
実験では、どちらがどのように違うかわからないから実験するので、片側検定を使うことは滅多にないと覚えておくと良いでしょう。
(確率統計学は最初に立てる仮説によって採用する検定が異なるので注意が必要です。)
t検定の計算方法
t検定で、「差がある」と言うためには「p値」を計算します。
p値とは
「p値」とは、
帰無仮説の元で検定統計量がその値となる確率のこと。P値が小さいほど、検定統計量がその値となることはあまり起こりえないことを意味する。
ちょっとわかりにくいので、もっと砕けた考え方にすると
帰無仮説:薬剤A添加群とコントロール群で細胞数に差が無い
としたときに
薬剤A添加群とコントロール群で細胞数の平均値が同じになる「確率」
をP値と言います。
つまりP=0.05とは、
薬剤A添加群とコントロール群で細胞数に差が無いと仮定して、
100回比較実験をすると、5回は平均値が同じになる(5%の確率で同じ値を取る)
と言うことは、
薬剤A添加群とコントロール群は95%の確率で平均の値に差が出る(95%の確率でこの結果は信用できる)
ということになります。
t検定では、「p値」を直接算出できないので、t値を算出してから「p値」に変換します。
「p値」についてこちらの記事にまとめています。

p値を算出するためにt値を出す
t値とは2つのデータの平均値が“異なる”と言える条件を数値化したもの。
異なると言えるための条件は全部で3つあります。
- データの平均値が離れている
- データの平均値が信用できる(分散が小さい)
- サンプルの数が多い
これを数式化すると、
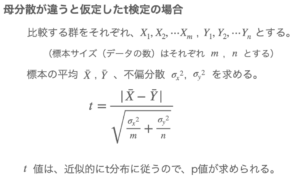
でも、t値がどれくらい大きければ「平均値に“有意な差”があるのか」はわかりにくいのです。3を超えれば大きいのか?100を超えないのダメなのか?よくわかりません。
t値をp値に換します。(変換はPCで簡単にできます。数式は複雑なので知らなくても大丈夫です!)
出した実験データの検定にt検定は使えるのか?
では、実験で出てきたデータの検定にt検定は使えるのか?を検討してみましょう。
t検定を使えるかどうか?の検討方法を下のフローチャートにまとめました。
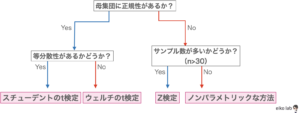
サンプル数が多かった場合(一般的にはサンプル数が30より多い場合)、
中心極限定理から、標本の平均が正規分布に近づいていくためZ検定で近似値を算出できる。
サンプル数が少ない場合、
ノンパラメトリックな方法(マンホイットニーのU検定など)で検定を行います。
今回、検証しようとしているサンプルを上のフローチャートに当てはめてみると、
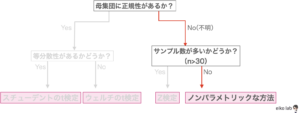
結果的にはt検定ではなく、ノンパラメトリックな方法を使うことになりそうです。
(母集団の正規性を確かめる検定ができれば、変わるかも知れませんが...)
中心極限定理とは?はこちらにまとめています。

パラメトリックな検定・ノンパラメトリックな検定についてはこちらにまとめています。

実験でのサンプル数(N数)については、こちらにまとめています。

【生命科学系のための統計】t検定って何だっけ? まとめ
t検定についてまとめておきます。
- t検定は母集団の平均値が同じかどうかを確かめる確率検定
- 母集団が正規分布であればt検定を使うことができる
(母集団の正規性を確かめる検定がある) - 集団の等分散性が確かめられれば、スチューデントのt検定、等分散でない場合はウェルチのt検定を使う
(等分散性があってもウェルチのt検定を使うのが一般的になっている) - データを出して、「とりあえずt検定」は間違っている場合もある
















