
実験データを示すとき、あなたはどんなグラフを使いますか?
もちろん実験系によって様々です。
薬剤投与における継時的変化を追うのであれば折れ線グラフを、二つの群の分布の違いを表したいときには散布図を使ったりしますよね。
生命科学の世界で最も一般的行われるのは、「2つの群(もしくはそれ以上)のある値を比較する」こと。そのために棒グラフ+エラーバーと言うスタイルがよく使われています。
ここ最近、科学系の雑誌では棒グラフ+エラーバーはあまり推奨されなくなってきています。
と言うのも、エラーバーが示す標準偏差や標準誤差はデータの数が十分でありが正規分布であることが前提とされた値。生命科学の実験で繰り返しできるのもせいぜい3〜5回くらい。データが十分である根拠はどこにもないのです。
そこで棒グラフ+エラーバーではないデータの示し方の一つとして、「箱ひげ図」が注目されています。
少しずつですが「箱ひげ図」が書かれている論文が見られるようになってきています。
今回はその「箱ひげ図」の見方、どんなことに注目してデータを見れば良いのか?を中心にまとめていきます。
箱ひげ図を見るための基礎知識
そもそも、箱ひげ図ってどんな数値を使って描かれるものなのでしょう?
知っておきたいのがこの5つの言葉です。
最小値、最大値、第1四分位数、中央値、第3四分位数
最小値と最大値はデータの中で一番小さい値と一番大きい値と直感的にわかる人が多いかもしれません。
では中央値はどうでしょう?平均値と何が違うかお分かりになりますか?
と言うことで、第1四分位数、中央値、第3四分位数について簡単にまとめておきましょう。
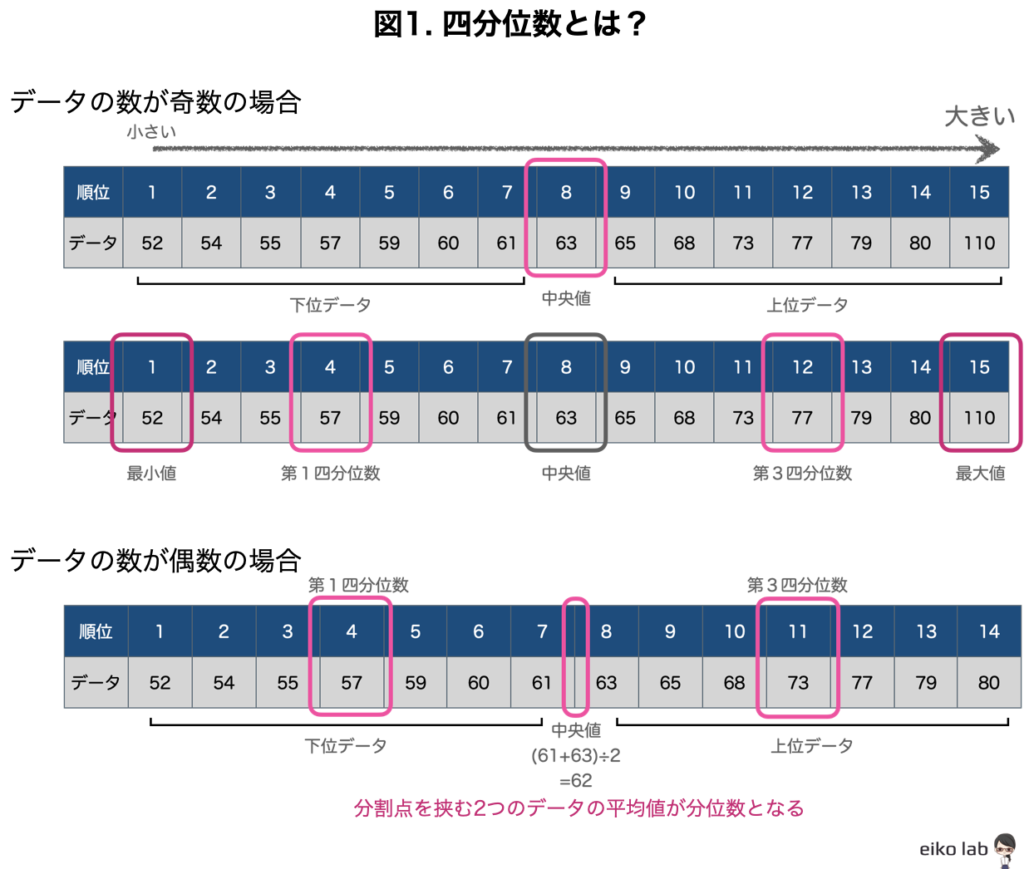
箱ひげ図を描くのに必要な四分位点(quartile)とは?
四分位点とは、データを小さいものから順番に並べて、データを四等分したときの3つの分割点のことを言います。この分割点に当たるデータをそれぞれ、第1四分位数、中央値、第3四分位数と言うのです。
第2四分位数(中央値)→下から50%目のデータの値
第3四分位数→下から75%目のデータの値
中央値と平均値は何が違うの?
四分位数の一つである中央値、平均値と何が違うのでしょう?
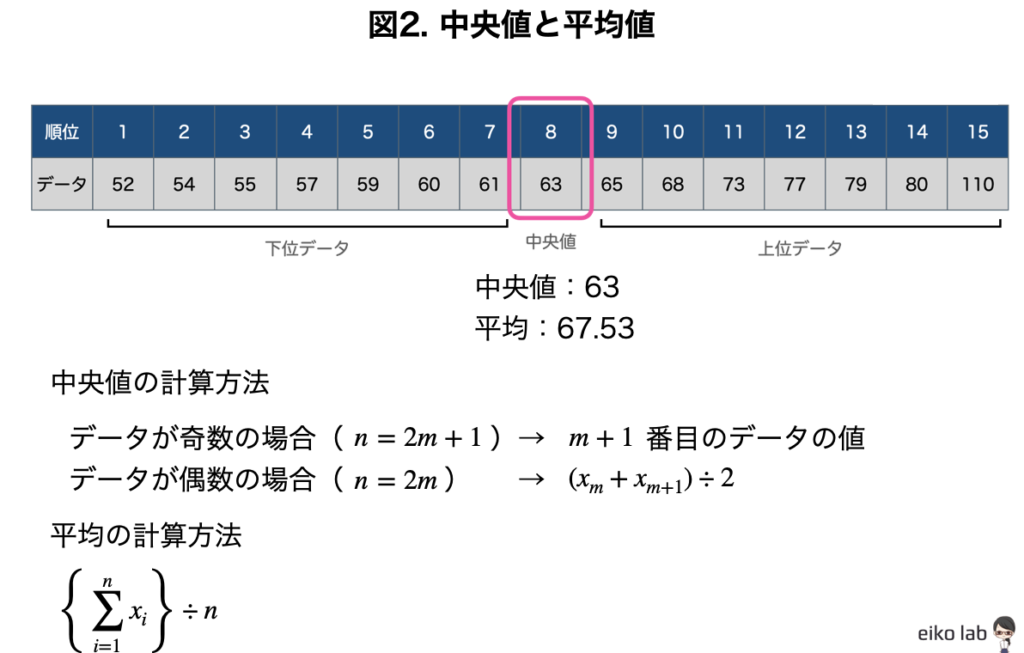
中央値(median)とは、
データの分布の中心。その値よりも小さなデータの数と大きなデータの数が同じになる値のことです。
平均値(mean)とは、算術的平均とも言われますが、
データの値を全て足して(総和)データの大きさで割った値のことです。
箱ひげ図の見方
ここまでは箱ひげ図を見るのに必要な知識をまとめてきました。
では実際に箱ひげ図を見てみることにしましょう。
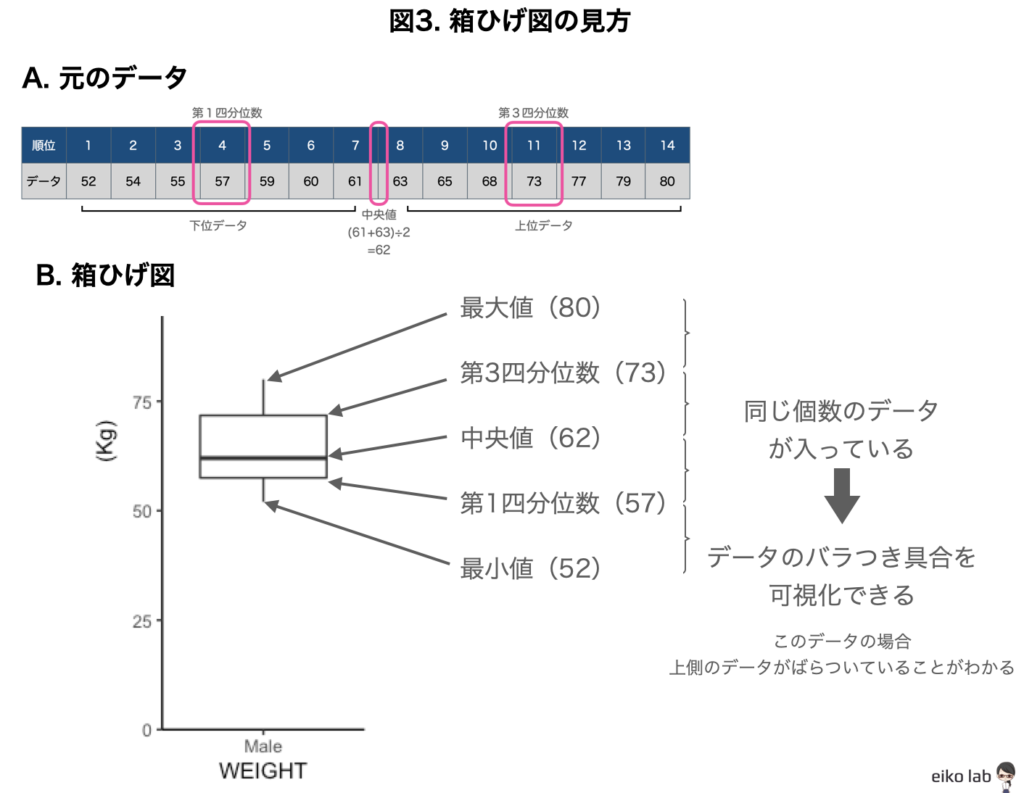
箱ひげの「ひげの長さ」は最大値から最小値の範囲を表しています。
箱の下側が第一四分位数、上側が第三四分位数、箱の上から下までの範囲のことを四分位範囲と言います。
ひげの下側から箱の下側まで、箱の下側から中央の線まで、中央の線から箱の上側まで、箱の上側からひげの上側までは、データの数が同じになっています。
箱の大きさ、ひげの長さからデータのバラつき具合を読み取ることができるのです。
外れ値がある箱ひげ図の見方
箱ひげ図の中には上側、もしくは下側に点が描いてある場合があります。この点は外れ値を示しています。
外れ値とは?
外れ値の定義は特にありません。とにかくデータ群から離れた値のことを「外れ値」と言います。(これでは納得いきませんよね!)
統計質保証推進協会主催の統計検定では、このように定められていました。
「第3四分位数」+「四分位範囲」×1.5以下の値まで
ひげを書き、これより外側の値を外れ値とする
この意味を図示してみましょう。
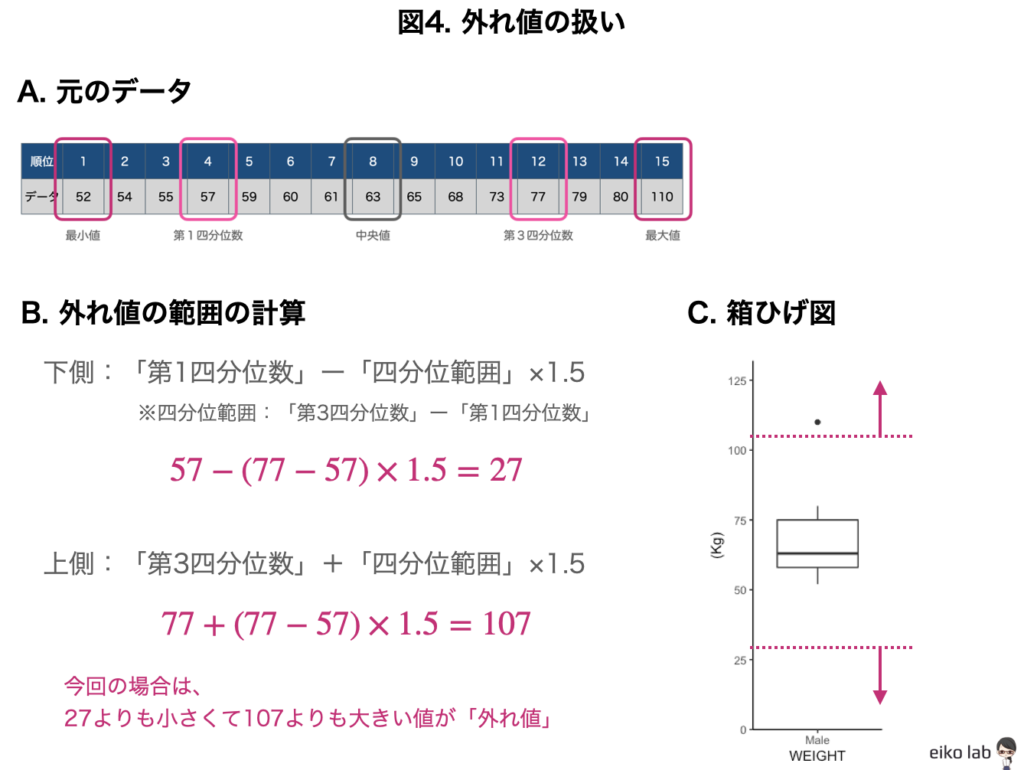
「外れ値」とされる範囲はかなりデータの中央から離れていることがわかりますね。
箱ひげ図ってどうやって描くの?
多くの生命科学系研究者はデータの管理にExcelを使っているように思います。
Excelで箱ひげ図が描けるようになったのはつい最近のこと。しかし実装されているフォーマットが扱いにくい印象です。
私はグラフを描くときは"R"を使っています。今回の記事でも示した箱ひげ図は全て"R"を使って描かれているのです!
Excelで描くよりも扱いやすいし、きれいに描けるのでオススメ。
次回は"R"を使った箱ひげ図についてまとめていきます。
-
- 箱ひげ図は「最大値」「最小値」「四分位数」を元に描かれる
- 一つ一つの区分には同じ数のデータが入っている
- データのバラつきを見るのに適している















