
生命科学のデータを出す時に、条件Aと条件Bを比較して違いがあるかどうかを示すことが多いのではないでしょうか?
例えば、「薬剤を添加したもの、添加していないもの」、「変異があるか、ないか」、「変異型、野生型」などなど...
一般的に「違いがあるかどうか」を示す時には、仮説検定が行われます。
よく知られているものに、t検定や分散分析(ANOVA)、回帰分析などが挙げられます。
今回はその仮説検定の中でも、2つの変数の関係があるかどうか?検定する「カイ二乗検定」について簡単にまとめていきます。
「仮説検定」とは?
「カイ二乗検定」の話に入る前に、「仮説検定」の考え方についておさらいします。
(簡単にするために統計学的な専門用語は使っていません)
「仮説検定の流れ」
- 検定を行う前に仮説(例:AとBに違いはない)を立てる
- 立てた仮説(例:AとBに違いはない)の下で出したデータが起こりうる確率を求める
- 起こりうる確率が高い場合は、立てた仮説が合っている(例:AとBに違いはない)
起こりうる確率が低い場合は、立てた仮説が間違っている(例:Aと Bに違いはある)
と言う過程を経て「違いがあるかどうか」を検証していきます。
「カイ二乗検定」とは?
「カイ二乗検定」とは、得られたデータが2つ以上の変数を持つときに、その変数の動きに関係があるかどうかを「分割表」を使って検証する検定方法です。
分割表を作るときに得られたデータ(観測値)と仮説の下で得られるであろう数値(期待度)の差の二乗の総和がカイ二乗分布のグラフに近似できると言う性質を使って検定を行います。
「カイ二乗検定」では、適合度(起こりうる比が想定と同じであるかどうか)と独立性(二つの変数の比が異なるかどうか)の検定ができます。
今回は、カイ二乗検定の中でも「独立性の検証」に焦点を当てていきます。
文字で書かれてもなんのことかよくわからないと思うので、想定実験を組んで話を進めていきましょう。
「疾患Xのモデルマウスを作製し、10週齢の時点で雄と雌の生存率を算出する」と言う実験を行ったとします。
データが下記の表のように得られました。

疾患Xは10週齢時点での雄と雌の生存率の違いを生み出すかどうか?を「カイ二乗検定」を使って検証していきましょう。
「カイ二乗検定」をする前に立てる仮説
「仮説検定」をする前には、「対立仮説」と「帰無仮説」を立てます。
「対立仮説」とは本来実証したい仮説。
「帰無仮説」とは「対立仮説」と反対の仮説。
今回の例で言うと、
「対立仮説」→「疾患Xは雄と雌の生存率に影響を与える(雄と雌で生存率が変わる)」
「帰無仮説」→「疾患Xは雄と雌の生存率に影響を与えない(雄と雌で生存率は変わらない)」
となります。
「帰無仮説」の下で検証を行い、そのデータが出てくる確率が高いか低いか?で仮説を採用するかどうかを決めていきます。
と言うことで、次に「確率が高いか?低いか?」の基準となる確率を決めていきます。
一般的に、この基準となる確率を「有意水準(α)」と呼んでいます。
有意水準は、本来示したい仮説と逆の条件(帰無仮説)の下で起こりうる確率なので、確率としてはかなり低いはずです。
一般的には5%(α=0.05)、1%(α=0.01)に設定されることが多いです。
α=0.05と言うことは、帰無仮説の元で100回データを得た場合、5回くらいしか起こらない出来事のことです。
今回は、有意水準(α)を0.05に設定しましょう。
帰無仮説のもとで算出した、データが得られる確率(統計量)が0.05よりも小さかった場合、「帰無仮説」は棄却されて「疾患Xは雄と雌の生存率に影響を与える(雄と雌で生存率が変わる)」と言います。
「カイ二乗検定」で算出する統計量
大まかな流れがわかったところで、作製した分割表をもとに統計量を計算していきましょう。
カイ二乗検定をするときに算出するのは、期待度数(得られたデータから推定できる期待値)と自由度、カイ二乗値です。
自由度については少し難しい概念なのですが、得たデータの規模がどれくらいか?を数値化したものだと思ってください。(カイ二乗分布は自由度によってかなり分布グラフの形が異なってくるので...データの規模に左右されやすいようです)
期待度数の算出方法
N人の標本によって得られるr(横)×c(縦)の分割表を考えます。
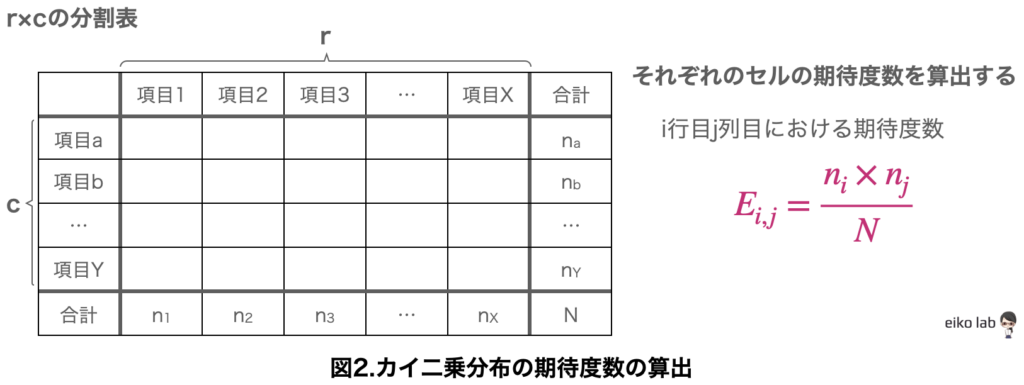
自由度の算出方法
自由度は以下の計算式を使って算出できます。
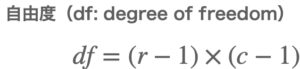
算出した自由度はカイ二乗分布とカイ二乗値との比較に使用します。
カイ二乗値の算出
カイ二乗値の算出方法は以下の通りです。
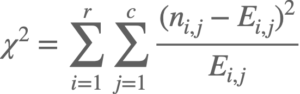
算出されたカイ二乗値から、起こりうる確率(P)をカイ二乗分布表を参照し、有意水準と比較します。
カイ二乗分布と自由度
カイ二乗分布は自由度によってかなり変わってきます。
自由度によるカイ二乗分布の違いを図でみてみましょう。
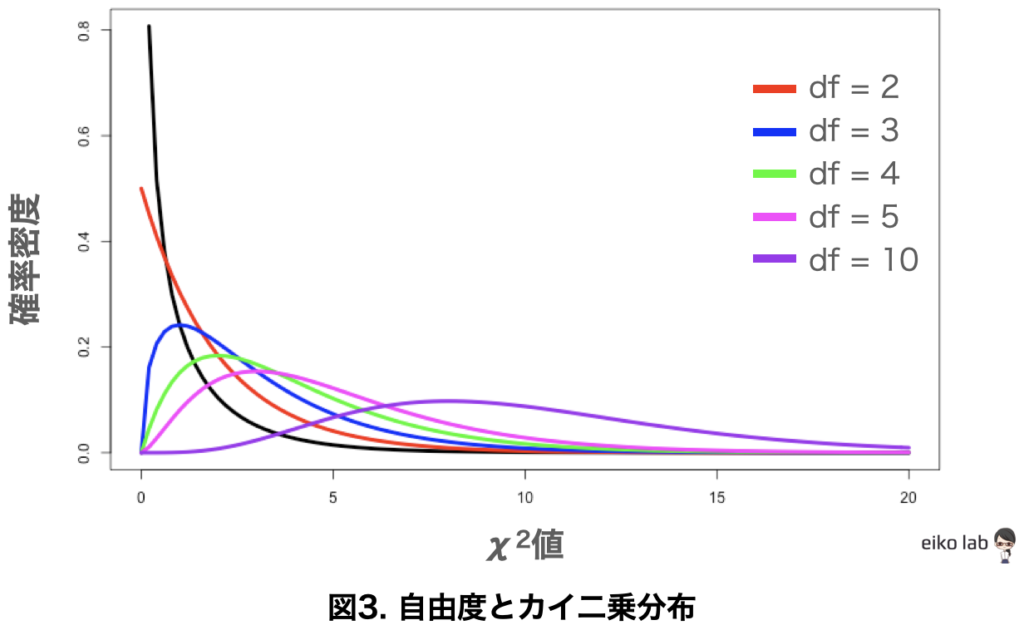
得られたデータから「カイ二乗検定」をしてみる
想定実験から得られたデータから、先ほどの手順で期待度数、自由度、カイ二乗値、起こりうる確率を算出してみましょう。
期待度数

自由度
得られたデータは2×2の分割表なので、先ほどの式に当てはめると...
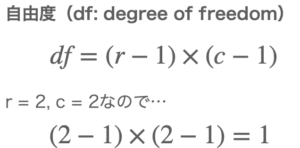
となります。
有意水準との比較
カイ二乗値を算出して、得られた確率を有意水準と比較していきましょう。
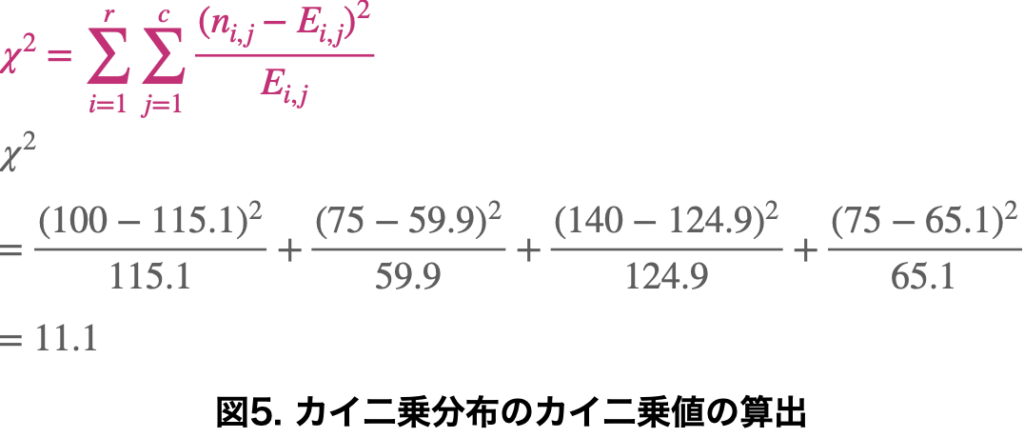
カイ二乗分布表と比較すると、有意水準が0.001よりも小さいことがわかりました。
Rを使って「カイ二乗検定」をしてみる
2×2の小さなデータであっても、かなりの計算量になることがわかったかと思います。
Rを使えばコードを二行書くだけであっという間に「カイ二乗検定」をすることができます。
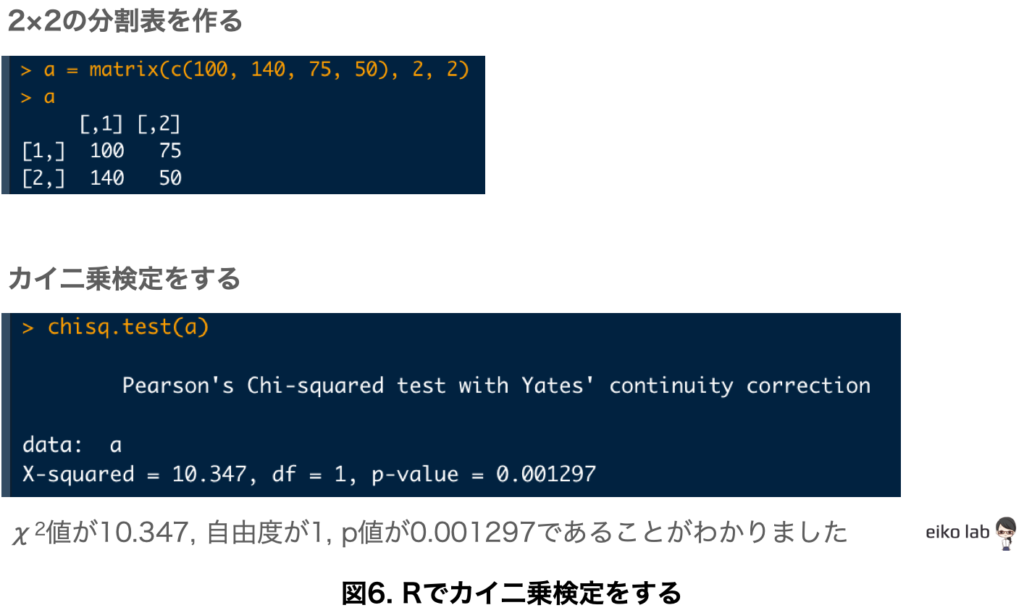
Rを使いたい!と思った方は、Rを使うための「RStudio」をインストールしましょう。
インストールの仕方はこちらの記事をご覧ください。
「カイ二乗検定」 まとめ
最後に、「カイ二乗検定」についてまとめておきましょう。
- 「カイ二乗検定」は2つの変数の独立性を検定する仮説検定
- 生命科学の分野では疾患と他のパラメーターの比較によく用いられる
- データの規模が小さい場合は手で計算できる
- Rを使えば簡単に検定できる
SNPsの解析であるGWASのデータ分析にも用いられる。
SNPsやGWASに関する記事はこちらにまとめています。
















